Area between Two Curves - Integration
Applet
Steps for constructing the applet
1.Open a new geogebra file
2.Create 3 sliders on number and give names a, c and m ( min: 0, Max : 10, Incr: 0.1 )
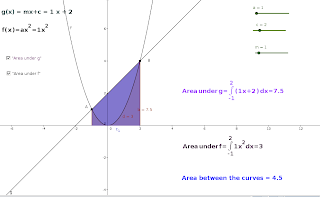
3.Create the function f ( f(x) = ax2 by typing in the Input field f(x) = a*x^2
4.Create the function g ( g(x) = mx + c by typing in the Input field g(x) = m*x + c
5.Mark the intersecting points A and B between the curve and the line using the tool Intersect Two objects
6.Create the number b which is the area between the curve g(x) and the x- axis by typing in the Input field Integral[g(x), x(A), x(B)]
7.Create the number d which is the area between the curve f(x) and the x- axis by typing in the Input field Integral[f(x), x(A), x(B)]
8.Use the tool Insert Text and and type the following text “g(x) = mx+c = ” + m + “x + c
9.Create the Checkbox e and give it the caption “Area under g ”. From the drop down menu add “Number b : Integral of g from x(A) to x(B)”
10.Use the tool Insert Text and and type the following text "f(x) =ax^2 = " + a + " x ^2"
11.Create the Checkbox h and give it the caption “Area under f ”. From the drop down menu add “Number d : Integral of f from x(A) to x(B)”
12.Use the tool Insert Text and and type the following text "Area \,under \, g = \int_{" + (x(A)) + "}^{" + (x(B)) + "}(" + m + "x +" + c + ")\,dx = " + b
13.Use the tool Insert Text and and type the following text "Area \, under \, f = \int_{" + (x(A)) + "} ^ {" + (x(B)) + "} " + a + "x^2dx =" + d
14.Use the tool Insert Text and and type the following text "Area between the curves = " + (b - d)
